MATEMÁTICAS 3º B

 

LA MULTIPLICACIÓN POR 2 NÚMEROS

La regla para multiplicar por dos números es 

muy sencilla, porque ya sabéis multiplicar 

por una. Así que no os compliquéis y ya veréis que tengo razón. Eso sí, hay que saber bien las tablas que lleváis estudiando desde principios de curso.

Lo mejor es ver el ejemplo de la izquierda.

Fijaos que lo que hice fue multiplicar primero 54 x 5 y debajo 

54 x 1. Pero, como os dije en clase, al multiplicar por el segundo número (en este  caso el 1) tengo que dejar libre un espacio. Fijaos 

que NO coloco los números de la segunda fila justo debajo  del 0, 

sino que empiezo debajo del 7. ¿Qué hay que tener en cuenta 

también? pues con las que nos llevamos y no olvidarnos de sumarlas 

al multiplicar el siguiente número.

Ved el siguiente vídeo.

   ------oo000oo------

    LAS POTENCIAS

Vamos a hablar aquí de algo nuevo como son las potencias. Antes de nada vamos a aprender lo que son.

Las potencias son una manera abreviada de escribir una multiplicación formada por varios números iguales. Son muy útiles para simplificar multiplicaciones donde se repite el mismo número. Las potencias están formadas por la base y por el exponente.

Veamos:

Esto es lo que venimos haciendo en clase a la hora de trabajar con ellas. Sin duda es una forma abreviada de escribir una multiplicación ya que al escribir 23 (Aquí pongo el exponente "3" en la parte de abajo porque el ordenador no me deja colocarlo en la parte superior) es lo mismo que si escribo: 2 x 2 x 2. Es decir, que el exponente (número pequeño) nos indica el número de veces que tengo que multiplicar el 2 (base) por sí mismo.

Más ejemplos: (vosotros el exponente colocarlo en la parte superior)

34 = 3 x 3 x 3 x 3 (El resultado sería "81")

52 = 5 x 5 (El resultado sería "25")

63 = 6 x 6 x 6 (El resultado sería "216") 

 

Así va a ser siempre.

En cuanto a la lectura de las potencias se dice de la siguiente forma: 

Cuando el exponente (número pequeño de la parte superior) 

es 2 se lee "al cuadrado"; si el exponente es 3 se lee "al cubo" y a partir de ahí se lee a la cuarta, a la quinta, etc.

32 = tres al cuadrado.

53 = cinco al cubo.

45 = cuatro a la quinta.

 ----oo000oo----

LA DIVISIÓN

Vamos a empezar a estudiar la división, y para ello tenemos que saber primero a qué se refiere el término "dividir". Dividir es repartir en partes iguales algo. 

Por ejemplo: si quiero compartir una pizza con 4 personas tendré que cortar 4 trozos iguales, uno para cada uno. Acabo de hacer un reparto igual, es decir, una división.

En el ejemplo de arriba vemos una serie de nombres que os pueden sonar raros al verlos por primera vez. 

Veamos:

-"Dividendo": es la cantidad a repartir.

-"Divisor": es el número entre los que se quiere repartir algo. 

 (Fijaos   que se coloca dentro de un casillero típico de la división.) 

-"Cociente": es el resultado de la división. 

-"Resto": se refiere al número de elementos que sobran.

*En el caso del resto puede que no sobre nada, es decir, "0" en este caso se dice que la división es "exacta". En el caso de que el resto no sea "0" sino 1, 2, etc. elementos, entonces se dice que la división es "entera".

Volviendo al ejemplo que os dejo, ¿de dónde salen esas cantidades?

Imaginaos que quiero repartir 45 caramelos entre 9 personas. Lo que tengo que hacer es ver qué número multiplicado por 9 se acerca lo máximo a 45; pues repasamos la tabla del 9 y el número que más se aproxima es el 5, ya que 9 x 5 = 45. Eso quiere decir que a cada uno de las 9 personas les daría 5 caramelos a cada uno. Y no me sobraría ninguno porque, fijaos, el resto es "0". En este caso decimos que la división es "exacta".

Repasamos el caso:

-45 caramelos sería el dividendo (lo que quiero repartir)

-9 sería el divisor (número de personas entre las que quiero

  repartir).

-5 sería el cociente (número de caramelos que le toca a cada

  persona)

-0 sería el resto (número de caramelos que sobran)

  Aquí os dejo un vídeo que os ayudará a entender lo que os digo

  arriba.

 PRUEBA DE LA DIVISIÓN

Si queremos comprobar si la división nos va bien podemos hacerlo mediante la "prueba". ¿Cómo se hace?  

COCIENTE x DIVISOR + RESTO (si es que lo hay)

Veamos:

66 : 7 = 9   Resto = 3

66 es el dividendo

7 es el divisor

9 es el cociente

3 es el resto

Pues si multiplico el cociente x divisor resulta esto: 9 x 7 = 63

Y si  a 63 le sumo el resto resulta que 63 + 3 = 66 (que es el DIVIDENDO)

*En este caso ya tenemos realizada la PRUEBA y vemos que está BIEN HECHA.

OS DEJO AQUÍ UN VÍDEO QUE OS PUEDE AYUDAR A DIVIDIR CON MÁS DE DOS CIFRAS EN EL DIVIDENDO. TAMBIÉN SE REALIZA  LA PRUEBA.

-----oooOOOooo----

Aquí os dejo cómo se suman y restan los números decimales, veréis que es muy fácil.

Y en este otro vídeo os dejo cómo se multiplica con decimales. Tampoco es difícil, lo que hay que hacer es NO DESPISTARSE.

-------oooOOOooo------

Como estamos estudiando "La masa", aquí os dejo unos vídeos que os pueden ayudar a comprender mejor lo explicado en clase.

En la siguiente tabla vamos a ver aquellas unidades de masa que son mayores que el gramo.

LA CAPACIDAD

¡¡¡YA VERÉIS QUÉ FÁCIL ES!!!

VAMOS A PRACTICAR UN POCO

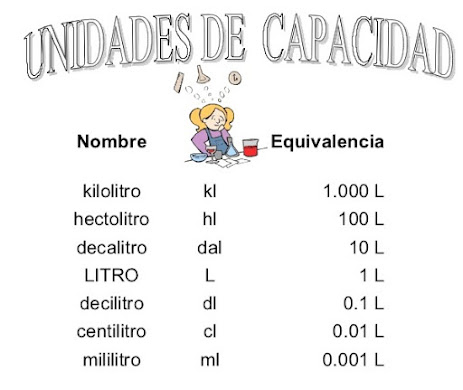
En la siguiente tabla vamos a ver aquellas unidades de capacidad que son mayores que el litro.

Para que os resulte un poco más fácil deciros que "deca" significa diez , "hecto" significa cien y "kilo" significa mil.  y todas estas palabras nos las dejaron los GRIEGOS.

UNIDADES DE LONGITUD

La unidad básica es el METRO. Recordad que estas unidades sirven para medir las cosas. Utilizamos una u otra dependiendo de lo que sea, por ejemplo: si medimos un lápiz utilizaremos el centímetro, pero si medimos a una persona utilizaremos el metro y si medimos algo muy pequeño utilizaremos el milímetro.

Veamos el siguiente vídeo que, como siempre, ayudará a comprender mejor.

En el vídeo de abajo vais a ver cómo se usa la regla para medir bien los objetos. Muchos ya lo sabréis, pero os sirve de repaso. 

"Expresiones complejas e incomplejas"

Para expresar la longitud se puede hacer de dos formas: de forma "compleja" y de forma "incompleja". Es más fácil de lo que os puede parecer, veréis.

Uno puede decir que la distancia desde su pueblo al pueblo vecino es de 5 km. 397 m. (Lo está expresando de forma compleja), pero puede expresar lo mismo de forma diferente, así: que la distancia entre los dos pueblos es de 5397m (lo está expresando de forma incompleja). Para resumir: si la distancia la expresa en más de una unidad (km. y m. por ejemplo) decimos que es en forma "compleja", y si la distancia la expresamos en una sola unidad (metros, por ejemplo) es cuando decimos que está expresada en forma "incompleja". 

"EL TIEMPO ES ORO"

Decimos que "el tiempo es oro" cuando queremos decir que no se debe desaprovechar. Por eso en clase debemos aprovechar el tiempo para saber cada día un poco más. Y, como vimos en estas últimas clases, el tiempo se puede medir, así que vamos a repasar la medición del mismo en el vídeo que viene a continuación.

Vamos ahora a ver los dos tipos de relojes que hay: el analógico (de agujas) y el digital (de números). Lo vais a entender viendo este otro vídeo que os dejo aquí.

RECTAS, SEMIRRECTAS Y SEGMENTOS

Antes de nada tenemos que saber que hay varios tipos de líneas como pueden ser: línea recta, línea curva y línea poligonal. Las dos primera son fáciles de entender. La línea poligonal es la que está formada por varias líneas rectas. Abajo tenéis un ejemplo.

   (Línea poligonal)

Vamos a repasar:

a) Línea recta es la que NO tiene ni principio ni fin.

b) Línea semirrecta es la que TIENE principio pero NO tiene fin.

c) Y el segmento es una recta que TIENE principio y TIENE fin, es decir, una recta entre dos puntos.

Ahora vamos a ver las posiciones que pueden tener dos rectas.

 a) Rectas paralelas: las que nunca se llegan a cortar (cruzar). Por ejemplo las que forman las vías del tren en un a recta que jamás se llegarían a juntarse.

b) Rectas perpendiculares: las que se cortan formando cuatro partes iguales. Por ejemplo las de la ventana de abajo que forma 4 cristales iguales. 

  

c) Rectas oblicuas: Son las que se cortan de cualquier otras forma.

*Oblicuo quiere decir que no es ni vertical ni horizontal.

LOS  ÁNGULOS

Veamos ahora lo que son los ángulos. Estos se forman cuando dos líneas rectas se cortan. Ahora hay que saber los tres tipos de ángulos más comunes que se forman que son: 

-Ángulo recto: es el formado por dos rectas perpendiculares, siendo una vertical y la otra horizontal. El rectángulo tiene cuatro ángulos rectos. 

 *La palabra rectángulo si os fijáis ya quiere decir "ángulo recto".

-Ángulo agudo: es el ángulo que es más cerrado que el ángulo recto.

El ángulo que forman las agujas del reloj es "agudo", porque es más cerrado que el recto que formarían , por ejemplo, al marcar las tres en punto.

-Ángulo obtuso: es el que es más abierto que el ángulo recto. Las agujas del reloj de abajo forman un ángulo "obtuso".

   

Todo esto puede parecer un poco complicado, pero ya veréis que es más fácil de lo que parece. Lo seguiremos viendo en clase poco a poco.

  MEDIDA DE LOS ÁNGULOS

En las figuras de arriba vemos los tres tipos de ángulos que estudiamos en clase. Empezamos, si os acordáis, por el ángulo recto, que es el del medio, y mide 90º. Luego seguimos por el primero que es un ángulo agudo y dijimos que medía menos de 90º. Por último nos queda el de la derecha que se llama ángulo obtuso y mide más de 90º. 

*Para medir los ángulos usamos el transportador de ángulos, que ya visteis que no es difícil de utilizar.